General information
General information
- The game’s board has two sides: one has a 10×10 squares field, the other, an 8×8 square field. The lesser field can be used to train or play shorter games.
- The kit is comprised of 160 double-sided chips with black and white sides. To play on the big field, 144 chips suffice. To play on the small field, 100 chips are enough.
- A sandglass is used if the game is played with limited time per turn
The goal of the game is to occupy as many field squares as possible with your team’s chips by effectively using the possibility to put, move and replace the opponent team’s chips with your own chips. The game is over when all board squares are occupied with chips. The team that has more chips on the main 10×10 field (or 8×8) in the end wins.
Teams can consist of 1, 2 or 3 people. Playing 3×3 is a classic version.
 CTOR game rules
CTOR game rules
The game begins with an empty field.
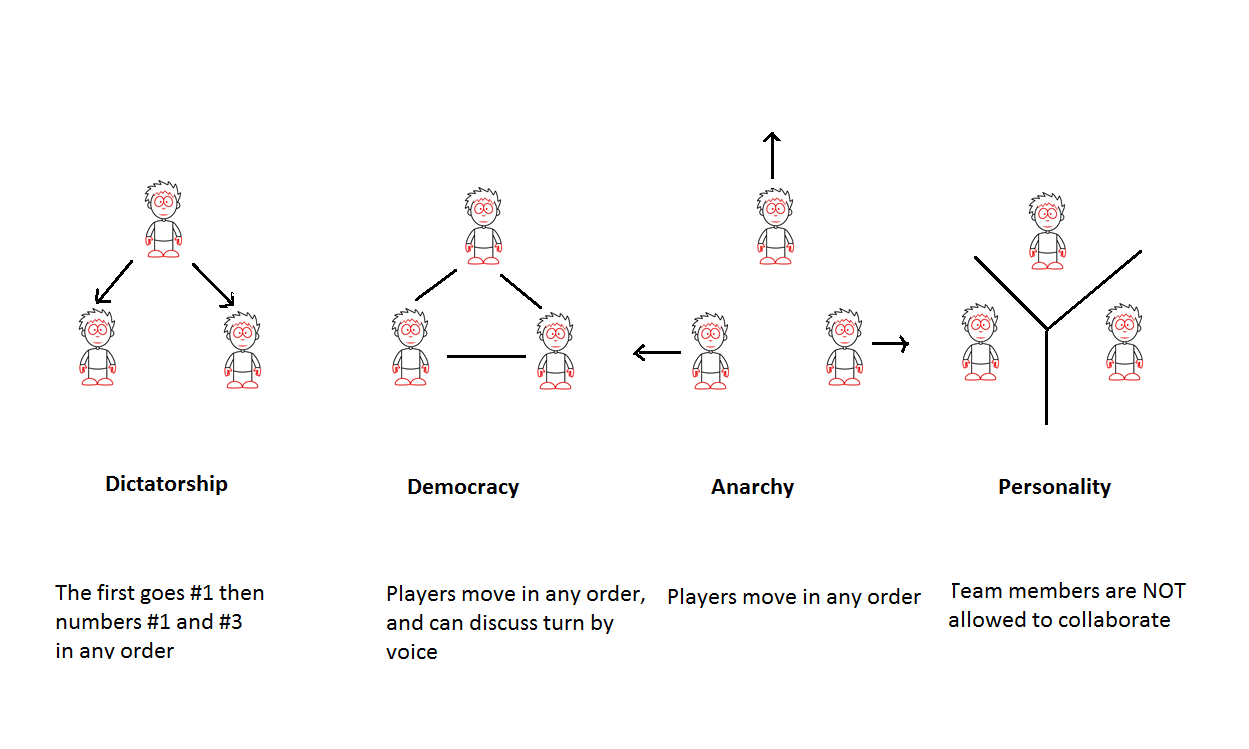
The CTOR game provides no ‘first turn advantage’. If the games is played 1 vs 1, 2 vs 2, or 1 vs 2, the team which has to play first puts 1 chip, then the second team puts 2 chips. If the games is played 1 vs 3, 2 vs 3, 3 vs 3, the first team puts 1 chip, the second team puts 2 chips, then the first team can put 3 chips. After these moves, the game goes back to regular rules (see Table).
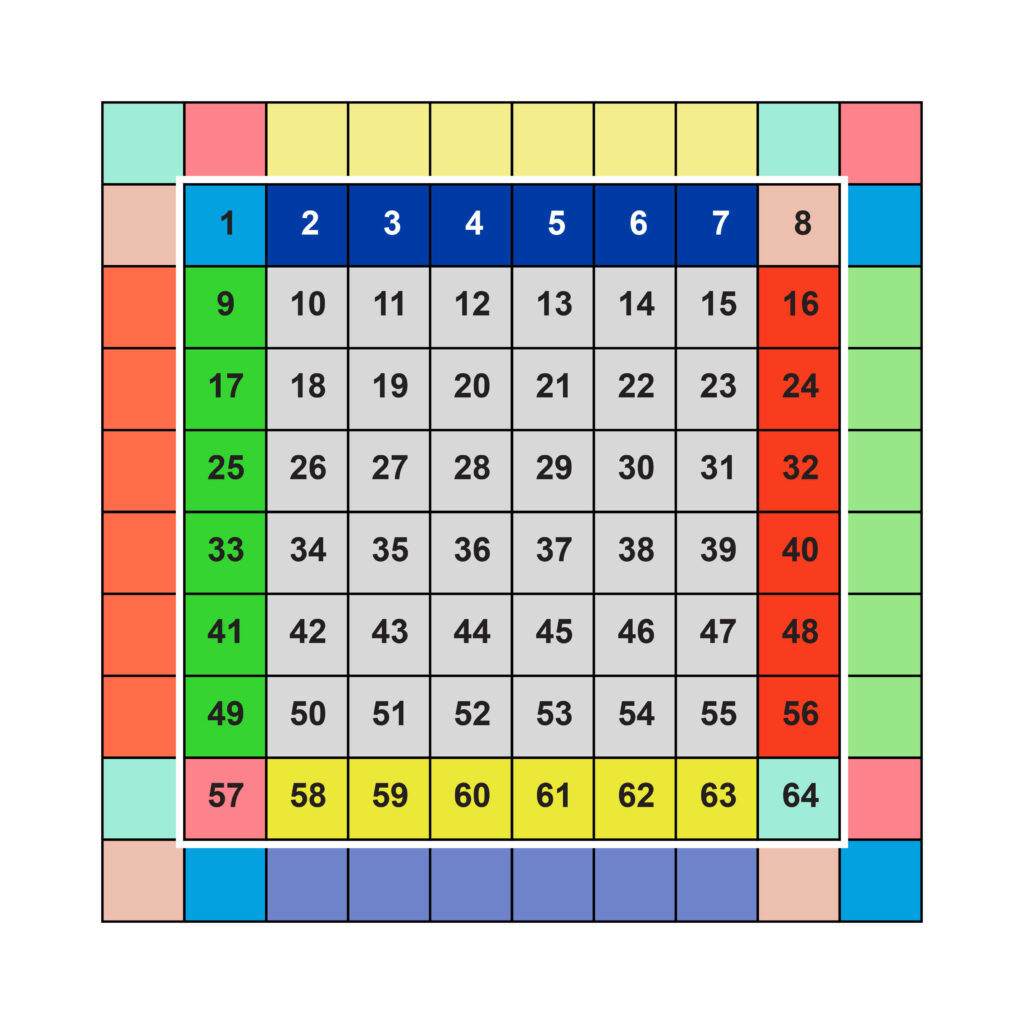
The game field consists of squares. Each square has its respective field coordinate represented by a unique number. On the 10×10 field, the squares bear numbers from 1 to 100; on the 8×8 field – from 1 to 64.
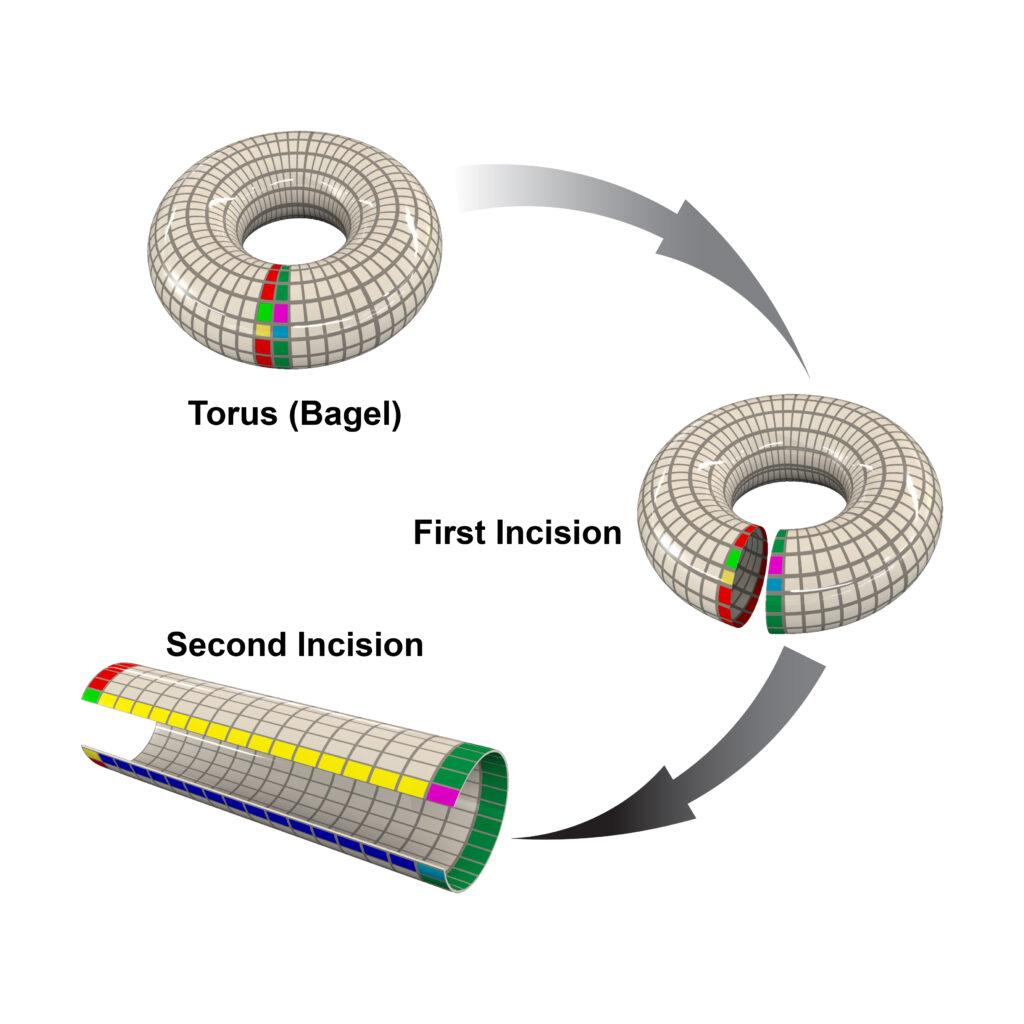
The field is a torus-shaped surface (doughnut) rolled out flat as shown in Fig. 1.

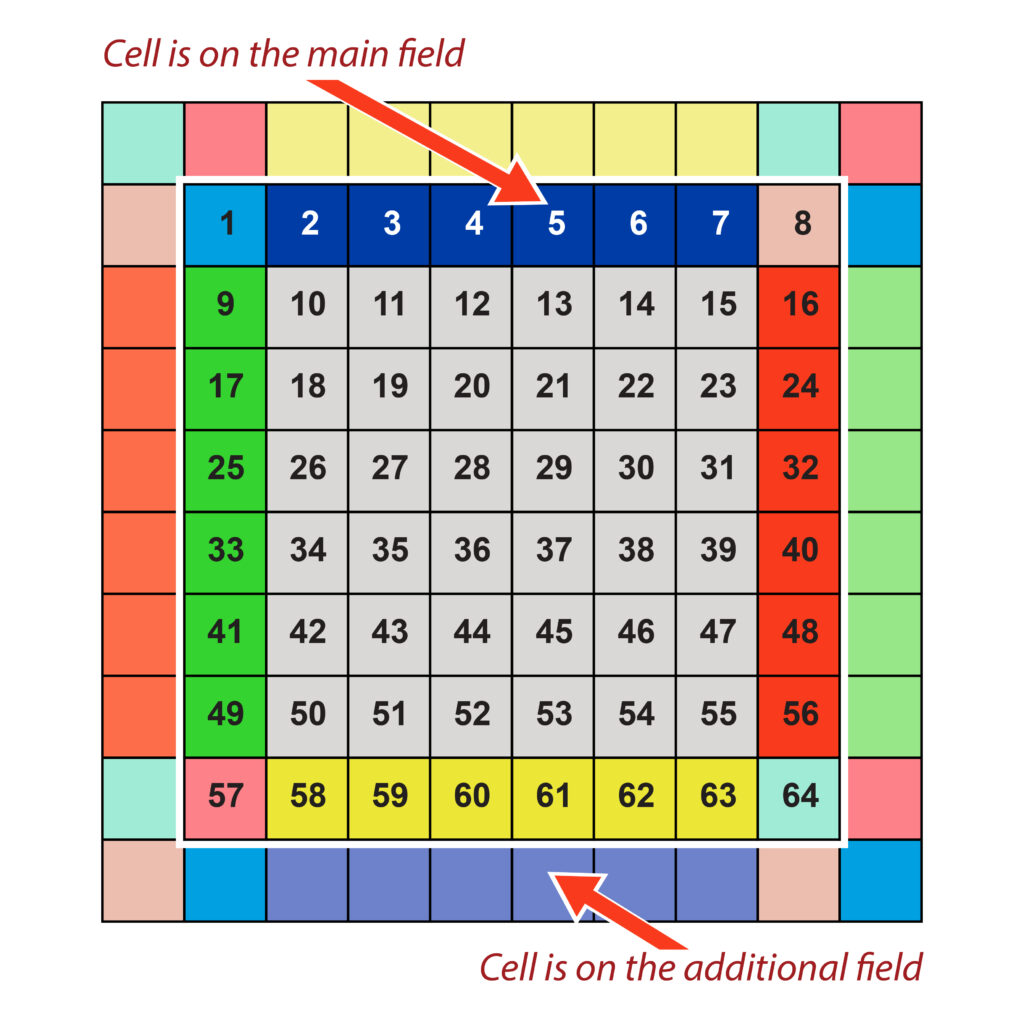
Squares along the field perimeter are auxiliary ones. They form an additional game field. They ‘duplicate’ squares of the main field on the other side. Fig. 2a shows a main square field (#5) and a corresponding additional square field.
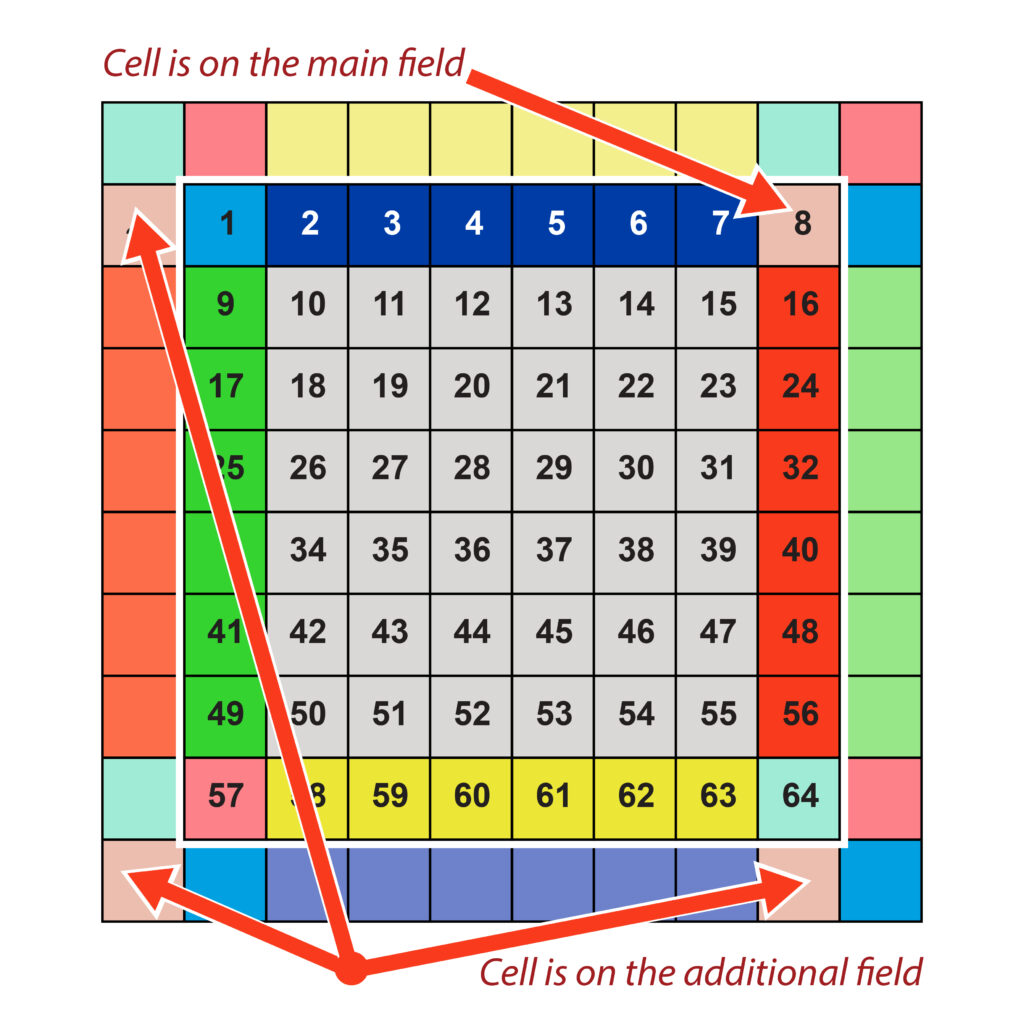
There is a total of 4 squares of this kind on the main field: No. 1, 8, 57, 64, each having 3 ‘duplicate’ squares on the additional field (for 8×8 field).
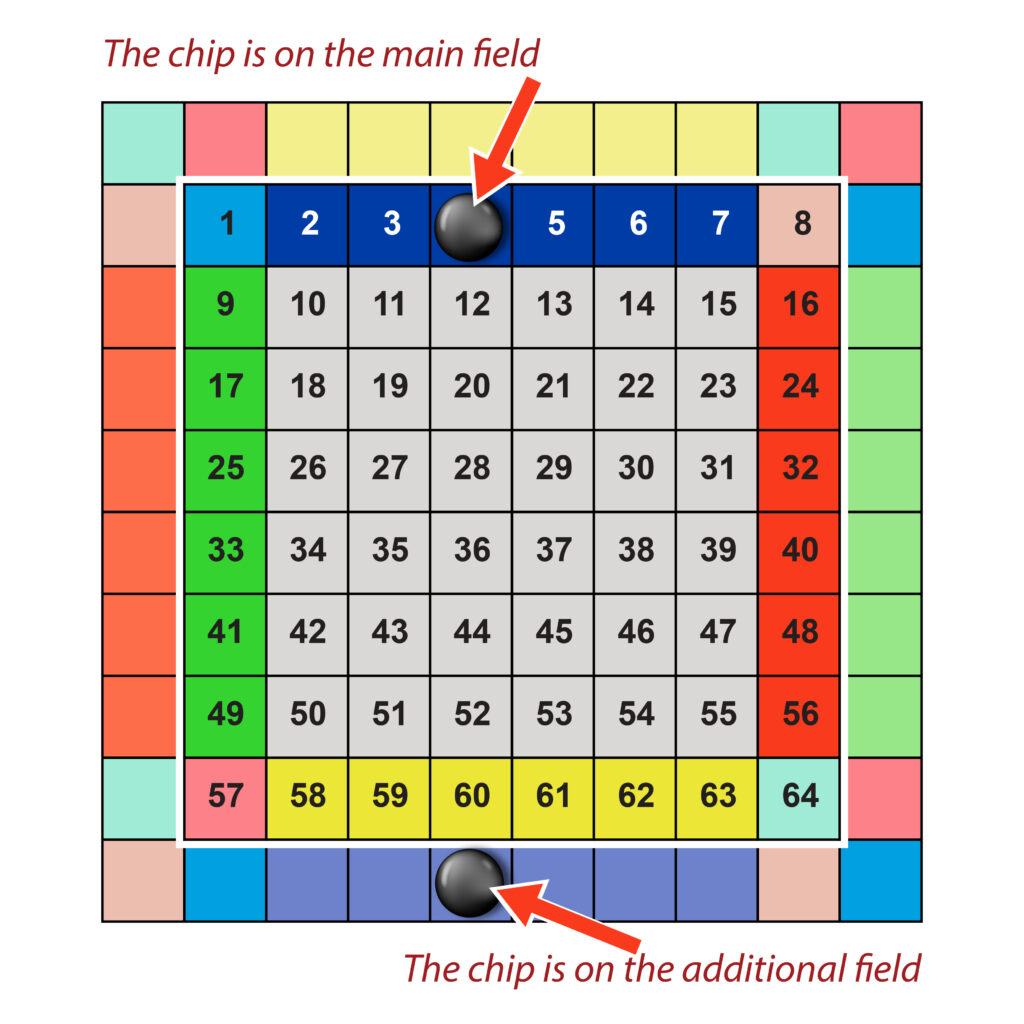
All manipulations with chips are performed on the main field. If a chip is put onto an edge square (#4) of the main field, its ‘duplicate’ is put on the opposite side, on the additional field (Fig. 3a).
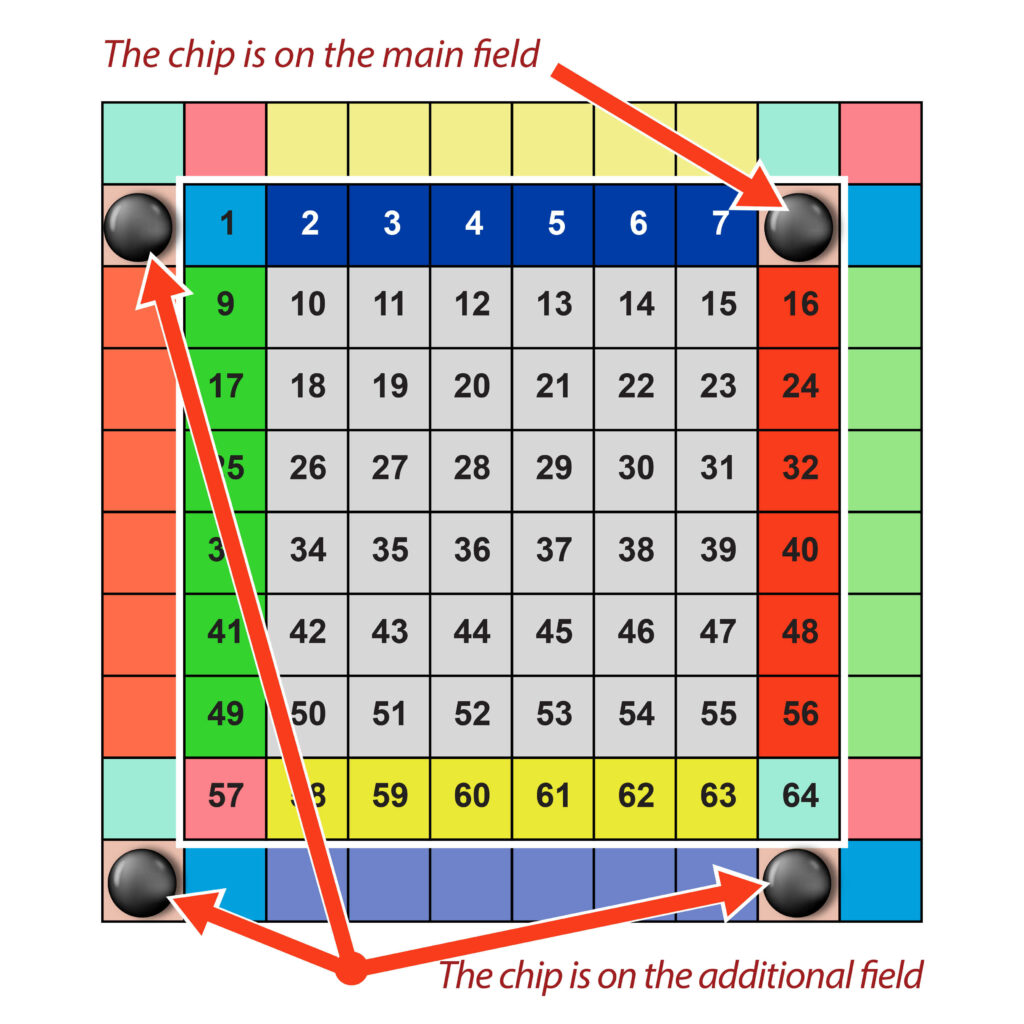
For side squares of the main field, one duplicate is put; for corner squares No. 1, 8, 57, 64, three additional duplicate chips for each one should be put (Fig. 3b).
Each turn consists of separate operations:
Put – putting a chip onto a free square of the main field and, if this is a color square, placing its duplicates on the additional field.
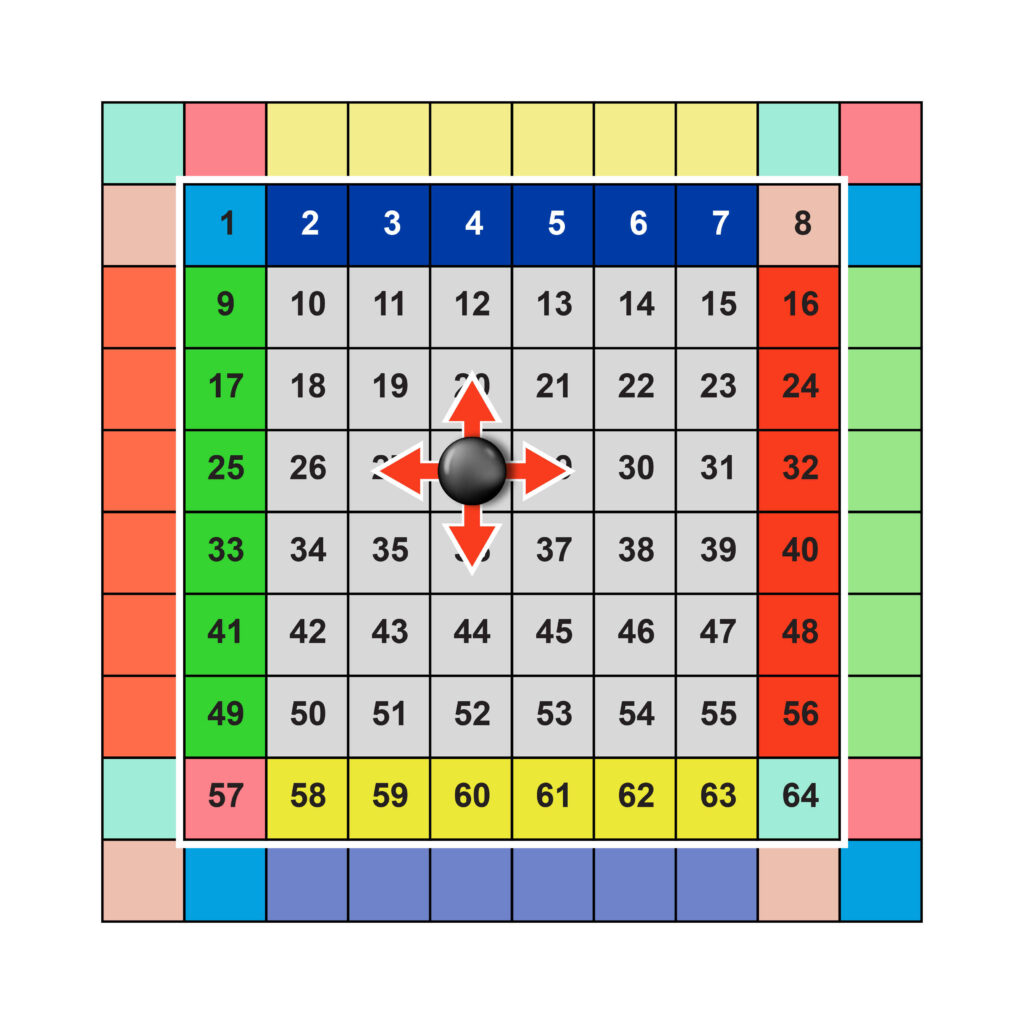
Move – moving a chip one square (#28) across the field in a horizontal or vertical direction (Fig. 4).
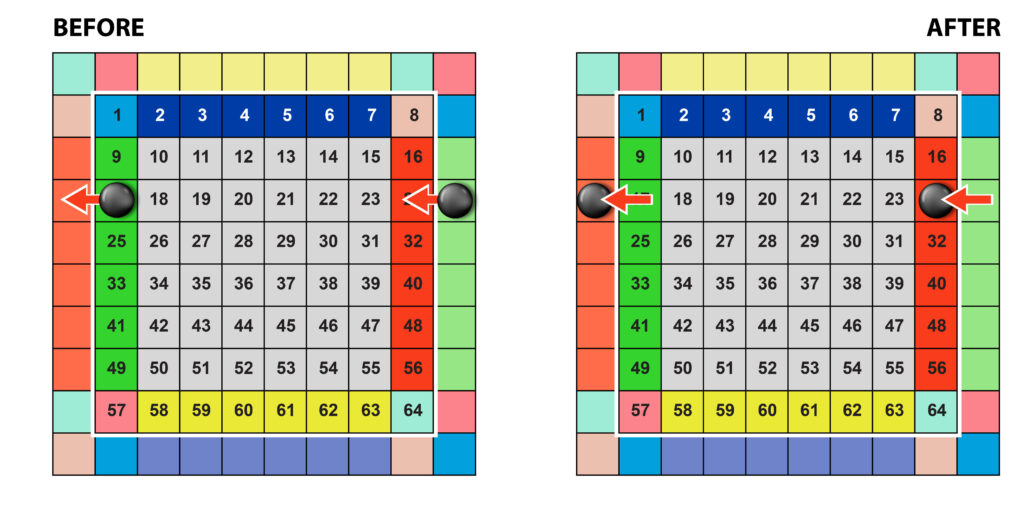
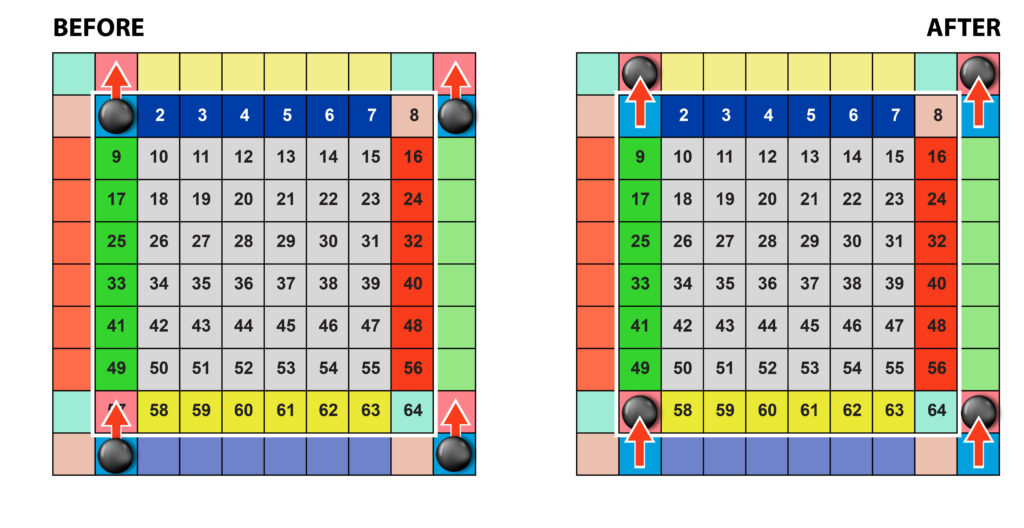
The same rule applies to duplicates of chips on field corner squares (Fig. 5b).
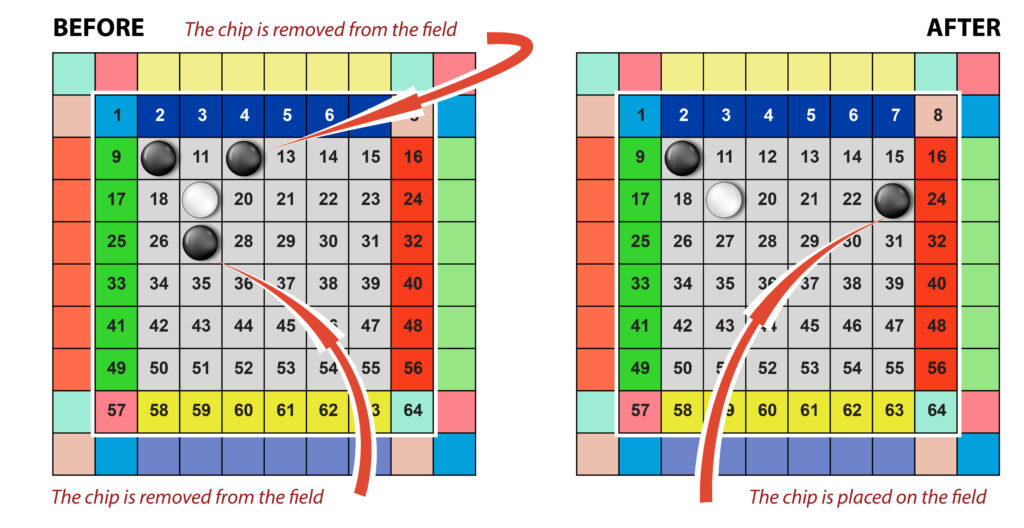
Landing – two of your chips (#19, #12) are removed from the field, and one chip (#23) of yours is placed on the field instead (Fig. 6).
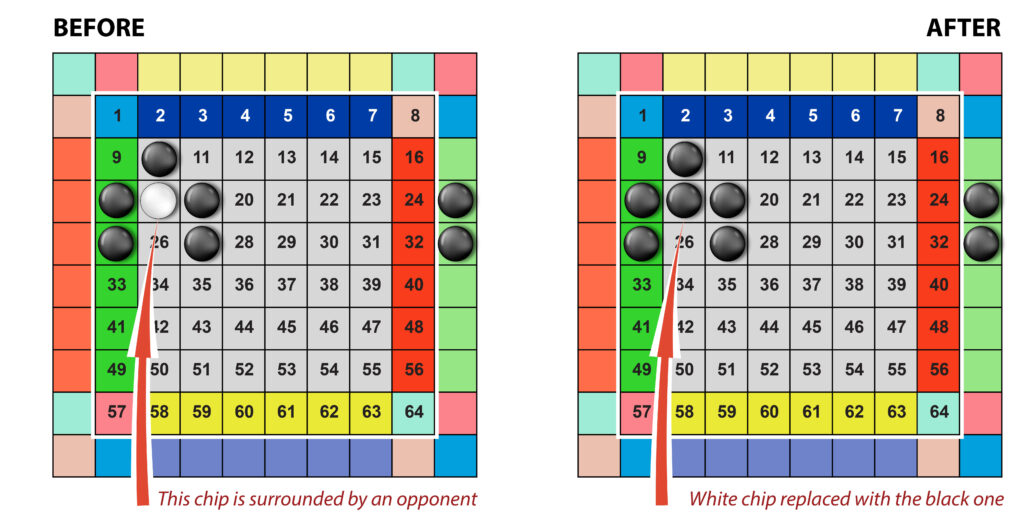
Replace – putting your chip instead of the opponent’s chip, if the latter is surrounded by at least five chips in any combination (in Fig. 7, a white chip is surrounded by 5 black ones).
Players perform operations (1-3) shown in the table below in turns, in any sequence. The Replace operation can be performed any time, upon completing one of the operations (1-3); the number of times is not limited. Players can skip operations if they believe it unnecessary at the moment. The team declares its turn completed and passes the turn to the opposing team.
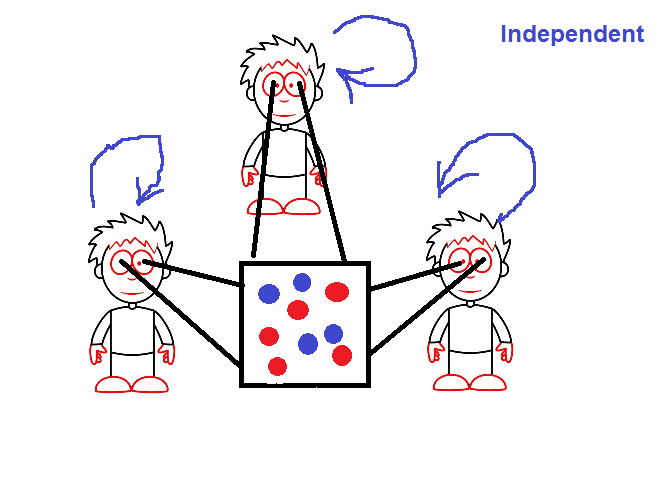
- A player chooses a square field for his/her next operation and notes its number on a sheet of paper not revealing it to other team players.
- Then, all players of the team open their selected square field numbers simultaneously and perform the operation.
- If two or more team players choose the same square for their current operation (the same coordinate), only one of them performs all operations with a chip on this square.
|
Team 1 |
Team 2 |
Put |
Move |
Landing |
|
1 |
1 |
2 |
2 |
1 |
|
2 |
2 |
2 |
2 |
0 |
|
3 |
3 |
3 |
3 |
0 |
 Team game options
Team game options
In this version, field square coordinates noted beforehand are used to work out the team’s general strategy before the game starts.
Before the game, each team notes five numbers of ‘secret’ field squares. If, when making its turn, the opponent chooses a secret square, the team’s chip is put on this field instead of the opponent’s chip. Afterwards, this chip is treated as a regular one. The substitution is made before the team starts its turn.
 Playing with incomplete teams
Playing with incomplete teams
The game can be played by unequal teams (e. g. 2 vs 3).
- If, with a selected turn power, e. g. 3, the game is played by teams 3 vs 3, and a member of a team quits, another team player assumes his/her duties and performs all operations for such player.
- To add a player to a team during the game, the number of players in this team should be less than the number of Put operations per turn. For example, if a team consists of 2 members, and this is a 3 vs 3 game, one person can be added to such team. However, if the team already consists of 3 players, adding a fourth one is impossible.
- For the team with more players, the following rule is applied. If, when performing a Put operation, a team player chooses the same coordinate as another team member, the player has the right to make another move, i. e. to choose another coordinate for this operation. This allows balancing chances of both teams as, if a player of the lesser team performs an operation twice, his/her team gets an advantage because there is no need to forecast the behavior of team players.